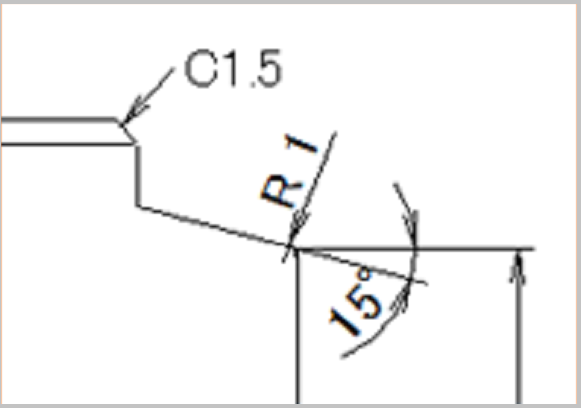
1. テーパーとは?
テーパーとは、円錐のような先細りになっている形のことをいい、加工部品でよくみられる形状です。
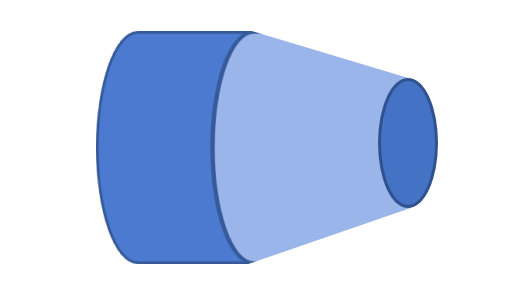
この形状だけを見ると、斜めに一直線に削られているだけで面倒な座標計算などは無いように見えるかもしれませんが、実際の図面ではそう簡単ではありません。
テーパーの開始位置、もしくは終了位置のどちらか一方の座標は図面から簡単に読み取ることができることが多いですが、もう片方の座標は図面に書かれている情報を元に、自分で計算する必要があります。
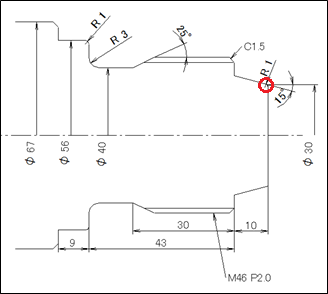
上の図面であれば、端面のZ軸座標を0とすると、
テーパー開始位置は(X30.0 , Z0) と簡単に分かりますが、終点は (X??? , Z-10.0) と、Z軸の座標は分かりますが、X軸の座標はテーパー角度と長手方向の長さから計算することでしか求めることができません。
多くの図面は、角度と長手方向の寸法で表されていますが、
「テーパー比率」や「勾配比率」で表されている図面もあります。
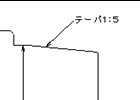
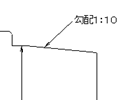
図2と図3の違いには注意が必要です。
図2のテーパー比率で表されている場合、こちらは直径で表記されていますので、5進んだら0.5(1の半分)上がる勾配と考えれば良いわけです。
一方、勾配1:10で表されている場合は、半径で考えるので、10進んだら1上がる勾配であることを示しています。
つまり、図2のテーパー1:5は角度にすると5.7105°、図3の勾配1:10も5.7105°となり、図面に書かれている比率は違いますが、同じ角度のテーパーであることを表しています。
2. 座標計算には三角関数が必須
三角関数と聞いて、高校生の数学の授業を思い出した方も多いのではないでしょうか?
テーパーの座標計算には三角関数の活用が必須です。
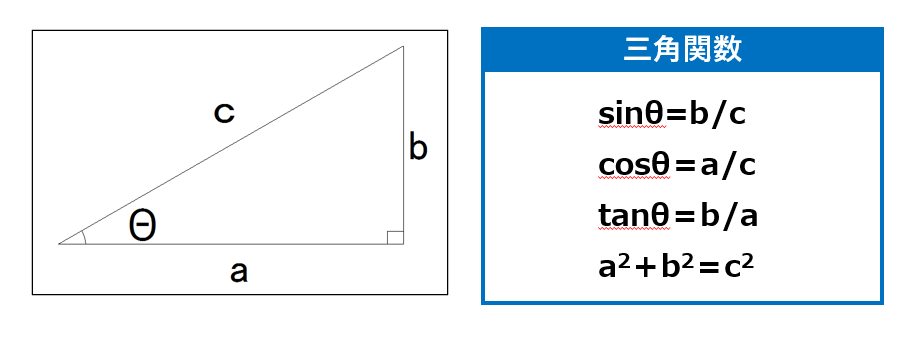
基本的な公式は以下に示した通りです。
数学の問題と実際の図面の大きな違いは、角度θが30°や45°といった数値を算出しやすい値ではないことです。
「tan15°= ?」と言われてもすぐに答えられないように、角度θが分かっていたとしても、sinθ,cosθ,tanθの値を自力で求めることは困難なので、関数電卓を準備して計算しましょう。
3. 図面で計算してみよう!
それでは先ほどの図面で実際に計算してみましょう。
こちらの図面の終点に当たる座標を求めます。
始点は図面より(X30.0 , Z0) であることは判明しています。
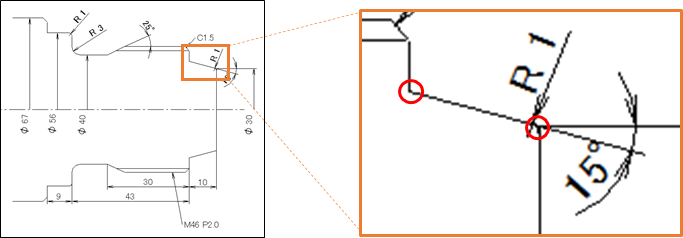
図面より、終点のZ座標は -10.0 と判明しているので、下に示した三角形をイメージしましょう。
この図ができれば三角関数「tanθ = b/a」を利用して、高さ(Z座標)を求めることができます。
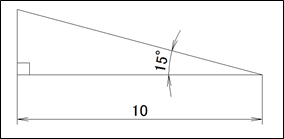
tan15°= b / 10
b = 0.267949 × 10 (関数電卓でtan15°を計算)
b = 2.67949上に示した三角形の高さは 2.6794であることが分かりました。
X軸の座標値は、直径値に変換(×2)して計算する必要がある点に注意し、X座標を計算すると
X = 30 + (2.67949 × 2) (×2して直径値に変換)
X = 35.359よって、終点の座標は (X35.359 , Z-10.0) と求められます。
今回のように、図面上で三角関数をうまく利用できる箇所を探し出すことが大きなポイントです。
そのためには、正しく作図を行うことが最初のスタートです。
どの三角形を使って考えるかを見極めてしまえば、求めたい辺に合わせて三角関数の式を活用することで値を求めることができるでしょう。
4. 実際の加工にはさらに多くの計算が必要
今回計算したはのはテーパー部分の計算のごく一部に過ぎません。
実際には、今回行ったテーパー座標の計算に加え、
・R部分の計算 (部品の角を丸くする処理)
・刃先 r を考慮した計算 (刃先の丸み)
これらが必要になります。
テーパー座標に比べれば細かい点ではありますが、実際の加工を行うには際には欠かせない要素です。
これらの計算を行わずに加工を行うと、実際の寸法よりも少し大きな部品が出来上がってしまいます。(削る量が少なくなる)
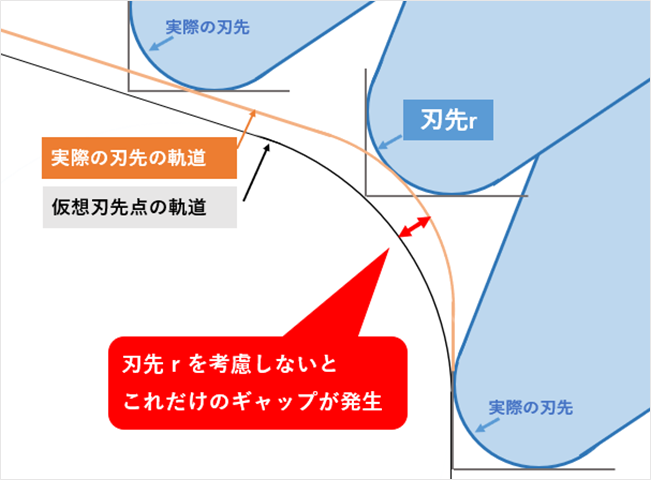
今回紹介したテーパーの座標計算に加え、「テーパーR部分の座標計算」「刃先rを考慮した座標計算」の方法についてはこちらの資料にて詳しく解説を行っております。
座標計算について詳しく知りたい、理解を深めたいという方は是非ご活用ください。
5. まとめ
今回はテーパー部分の座標計算について解説しました。
テーパーの座標計算は、
三角関数をうまく活用できる箇所を探し出しだせるかどうかが大きなポイントと言っていいでしょう。
また、X軸の座標値については直径値に直す(×2)ということも忘れないようにしましょう。
近年のソフトウェアの発展により、手動で座標計算を行う機会はかなり減ってしまいました。
自動プログラミング機能を活用したり、CADで作図して座標点を取ったりと座標計算時間を短縮できるツールを活用することはもちろん大切です。しかし、手動で計算できる知識を持った上で便利なツールを使うとなお良いでしょう。
テーパーの座標計算について、もっと細かい部分の計算まで知りたいという方はぜひ資料もダウンロードしてみてください。